こんにちは、バラ十字会の本庄です。
東京板橋では昨日今日と晴天が続き、歩いていて汗ばむほどの陽気です。
いかがお過ごしでしょうか。
4年前に下記のフェイスブックページを開設したときに、読者の皆さんに喜んでいただこうと、折々に道端の風景を写真に撮ってご紹介することを始めました。道端の風景とは言っても、道路とビルばかりが目立つ東京ですので、どうしても草花や昆虫などの写真が多くなります。
( フェイスブックページ「あなたの人生を変える方法」: https://business.facebook.com/amorc.jpn )
そして、草花の形の複雑さや巧みさに感心する機会が増えました。
次の写真をご覧ください。ダリアの花、イタリアンパセリのつぼみ、サクラソウ、開きかけのバラの花です。
これらを見ていると、人にはなかなか思いつかないようなユニークな形に驚きます。そして、いったい、このようなデザインは、どのようなメカニズムでできあがっているのだろうかと思いを巡らすことがたびたびあります。




神聖幾何学という言葉をお聞きになったことがおありでしょうか。植物だけでなく、動物の体のデザイン、小さなものでは分子から、人体や川の流れ、大きくは大気の循環や銀河系の構造など、自然界や宇宙のあらゆるデザインは幾何学に従っています。
そして、古代ギリシャの哲学者、ピュタゴラスやユークリッドやタレスのような人たちは、古代エジプトの神秘学派から数学を学び、自然界に、数学にもとづいた規則正しさがどのように表れているかを盛んに研究しました。
中世のヨーロッパでは、コンパスと目盛りのない定規だけを使う幾何学が、数学の中でも特に尊い学問だと考えられ、神聖幾何学と呼ばれていました。そして、それが自然界にどのように表れているかを調べることに加えて、建築や他の芸術に生かす研究が行なわれていました。
神聖幾何学の研究には、専門家でなければとても理解できないような複雑なものもありますが、誰にも理解できるものもあります。
そのうちの、最近知ったあるひとつの事柄が印象的でしたので、ご紹介させていただきたいと思ったのです。
まず準備として、クイズをひとつ解いてみてください。
1,1,2,3,5,8,13,21,34,55,・・・
この列の55の次にくる数は何でしょうか…
はい、この列では、前の2つの数を加えると次の数になるので、答えは、
34+55=89となります。
この数列は、12世紀のイタリアの数学者フィボナッチが著書「算盤の書」で紹介したので、フィボナッチ数列と呼ばれています。この数列に表れる数はフィボナッチ数と呼ばれています。たとえば、34や55、89はフィボナッチ数です。
次の松かさの写真を見てください。規則正しい美しいデザインですね。この写真の中央より、ほんの少し右下のあたりには、柄が付いていた場所があるのが分かります。そこから、鱗片が放射状に並んでいて、外側に進むにつれて右にカーブする「らせん」を描いています。

一方で見方を変えると、この鱗片の配置は、外側に進むにつれて左にカーブする、もっと長い「らせん」を描いていると考えることもできます。
このらせんは、対数らせんという種類のらせんだということが知られています。巻貝、牛の角、低気圧内の雲の形、銀河系の星の分布など、自然界のあらゆるところに、この対数らせんが見られます。

This Wikipedia and Wikimedia Commons image is from the user Chris 73 and is freely available at //commons.wikimedia.org/wiki/File:NautilusCutawayLogarithmicSpiral.jpg under the creative commons cc-by-sa 3.0license.
渦巻き銀河M51
By NASA, ESA, S. Beckwith (STScI), and The Hubble Heritage Team STScI/AURA) [CC BY 3.0 (http://creativecommons.org/licenses/by/3.0)], via Wikimedia Commons
さて、この松かさの「らせん」の本数を数えてみていただきたいのです。右にカーブするらせんは何本あるでしょうか。左にカーブするらせんは何本あるでしょうか。
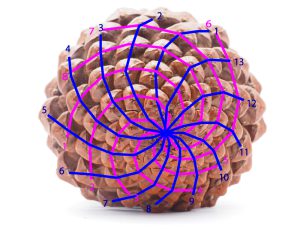
次の写真は、それを数えてみた図です。右カーブのらせん(青)は13本、左カーブのらせん(ピンク)は8本あります。いずれもフィボナッチ数になっています。
このことは、単なる偶然ではありません。その証拠に、次の写真を見てください。小さなヒマワリの花の中央に多くの種が美しく並んでいます。そしてこの種も、先ほどの松かさの鱗片と同じようなデザインに従って配置されています。

写真を拡大して印刷して、ひとつひとつ数えていくと、ちょっと楽しいひとときになります(私だけでしょうか?)。そして、左カーブのらせんが55本、右カーブが34本あり、いずれもフィボナッチ数であることが確かめられます。
次の写真は、もっと大きなヒマワリの花です。こうなると数えるのは、ちょっとたいへんですが、右カーブのらせんが89本、左カーブが55本と、やはりいずれもフィボナッチ数になっています。

以上、松かさもヒマワリも、数学をしていることが確かめられました。
対数らせんとフィボナッチ数列には密接な関係があることが知られています。次の図は、この関係を直観的に表わしています。
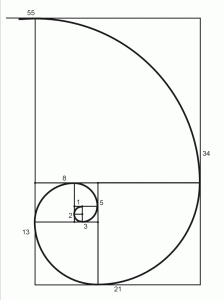
いかがでしたでしょうか。以上、神聖幾何学にまつわる、ちょっとしたご紹介でした。楽しんでいただけたなら嬉しく思います。
それでは、また。
追伸:メールマガジン「神秘学が伝える人生を変えるヒント」に、こちらから登録すると、このブログに掲載される記事を、無料で定期購読することができます(いつでも配信解除できます)。












コメントは受け付けていません。