こんにちは。バラ十字会の本庄です。
東京板橋では、一昨日、昨日と、かなり激しい雷雨でした。今日は今のところ、どうにか落ち着いているようです。
ほんとうに暑いですね。いかがお過ごしでしょうか。
さて、大阪で当会の役員をされている作編曲家の渡辺さんから『数とは何か?』の第2回の寄稿をいただきましたので、ご紹介します。
前回の記事はこちらです。
▽ ▽ ▽
数とは何か?(Vol.2)
~形而上学における数の概念~

前回は、「全体(1)」を「分割」するという考え方についてご説明しました。
今回は、さらにそれを掘り下げてみたいと思います。
■分割と周期 ~数が意味を持つとき~
「1、2、3、4…」と無限に続く数直線上の数字は、そのままでは、その数字自体にはあまり意味はありません。
そして、この数字自体も人間が作り出したものなので、単なるラベルであり、物を数えたりする(カウントする)場合には有用ですが、例えば「4」という数字には、通常はラベリングされた数字以上の意味はありません。
では、「数が意味を持つとき」とは、どのようなときでしょうか?
その重要な要素は、「周期」または「一単位」です。
言い方を変えると、時計のように使用する数字を「限る」とも言えます。

たとえば、「12」という数字は、それだけでは「12」番目などの意味しかありませんが、「一年(12か月)」という「周期」または「一単位」が与えられたときにはじめて、「12」をはじめ、その約数、倍数などの数が意味を持ち始めます。
■ 一年の分割
一年の「12」か月を一つの周期とすると、「24」という数は2年(2周期)、「6」という数は半年でちょうど一年の「1/2(半期)」を意味し、「4」という数は「3」か月と合わせて四季を意味します。
そして、立春、立秋などをあらわす「二十四節気」というものがありますが、これは一年を「24」分割して、約「15」日ごとに気候などが変わる様をあらわしています。
とても不思議なことに、上記のようにある周期が設定されると、数直線上では単なるラベルとしての意味しか持たなかった「6」や「4」、「24」などの数字は、一年を「全体(1)」として「12分割(12か月)」した瞬間から、「意味のある数」として、まるで生命を宿しているかのように生き生きと躍動し始めます。
同じように、数直線上では「7」番目という意味くらいしか持たない「7」という数字は、創世記に記された「7日(一週間)」という周期が与えられると、「安息日(※1)」として、カレンダー上では毎週訪れる「土曜日」という意味を持ちます。
(※1)安息日の定義は、宗教や時代によっても変わりますが、例として、日曜日から始まるものとして、7番目の土曜日を「安息日」として例示しています。
そして、たとえば、神が6日で天地創造を終えて7日目に休んだことから、「7」という数字を「神(完全)」を象徴する数であると仮定した場合、6日目に人間を作ったことから、「6」という数字は「人間(不完全)」を象徴する数とすることもでき、人間は「6(不完全)」から「7(完全)」へと至る存在として意味づけることもできますが、これは、使用する数字を1~7までに限った場合において、それぞれの数に象徴としての役割を与えることができるということを意味しています。
しかし、もし仮に、天地創造に9日を要したとすれば、どうなるでしょうか?
その場合、安息日は10日目となり、一週間は10日を一単位として考えられ、神を象徴する数字も「10」となります。
その場合、「7」という数字は、先ほどとは打って変わり、途端にそれほど重要な数ではなくなってしまいます。
このように、純粋に数学的な意味からではなくても、ある周期を与えられることによって、単なる記号に過ぎなかった数字たちは、「意味のある数」として、それぞれある特定の意味を持ち始めますが、それらはすべて、「どんな周期の上で語られるか」ということが重要になります。
■なぜ360度?
通常、私たちは円を360度に分割して考えますが、これは古代バビロニアから始まったと考えられています。
「なぜ、10分割や100分割ではないのか?」と一度は疑問に思った方も多いと思います。
実は、円を何分割したとしても「全体(1)」としての円の本質自体は変わりませんが、360という数は様々なパターンで等分することができ、とても扱いやすい数なのです。
それは、言い換えると「約数が多い」とも言えます。
円を360等分すると、1/2、1/3、1/4、1/5、1/6、1/8、1/9、1/10など、多くのパターンで等分することができます。
そして、1から10までの数のうちで、割り切れない数は7だけとなります。

では、100等分した場合はどうでしょうか?
等分できるのは、1/2、1/4、1/5、1/10などとなり、360で等分した場合に比べて少なく、そして、1から10までの数のうち、整数で割り切れる数は2、4、5、10となり、あまり使い勝手はよくありません。
ですから、太古の昔から人間は、「円(全体)」を様々に分割したいと考え、そして、それに適した「360」という数で円を分割するアイデアを思いついたのではないでしょうか?
■細胞分裂? 細胞分割?
実は、人間などの生命の発生過程の初期においても「分割」するという行為が行われています。
下図は、細胞が「分裂」する過程をあらわしていますが、よく見ると、実は「分裂」というよりも、「全体(1)」が「分割」されているということが分かります。
まさしく、「全体(1)」が1/2、1/4、1/8、1/16などに「分割」されているのです。
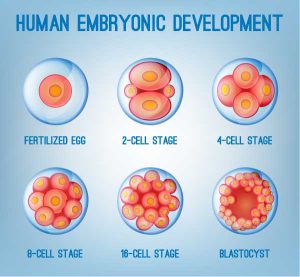
そして、見方を変えれば、「細胞が分裂を繰り返して増殖」するのではなく、「全体(1)が大きくなりながら分割され続けている」ということもできます。
■弦の分割
では、音で考えてみましょう。
あるギターの弦をどこも押さえずに鳴らし(例:220Hz)、その弦のちょうど半分の場所を押さえて鳴らすとちょうど1オクターブ上の音(440Hz)が出ます。
同じように、その押さえた場所からちょうど半分の場所を押さえて鳴らすと、元の音よりも2オクターブ上の音(880Hz)が出ます。
同一の弦の上で考えると、下表のようになります。
最初の音(開放弦) 1/2の場所 1/4の場所 1/8の場所
220Hz 440Hz 880Hz 1760Hz
基音 1オクターブ上 2オクターブ上 3オクターブ上
弦の長さを1/2にするごとに1オクターブ高くなり、周波数はその2倍になります。
そして、この比率は、どんな音の高さからスタートしても変わりません。
そして、これは、両端を固定した弦を「全体(1)」として、それを「分割」するという行為によって異なる高さの音を出していると言うことができ、最初の音(開放弦)よりも低い音を出すことはできません。

さて、駆け足で例を見てきましたが、「全体(1)」として例に挙げたものはすべて、始点と終点がある「閉じた世界(有限)」であることにお気づきでしたでしょうか?
これは、始点と終点がない「開いた世界(無限)」では、周期を設定することができないため、現実的には均等に分割できないということでもあります。
では、次回は、この「閉じた世界(有限)」と「開いた世界(無限)」について考察してみたいと思います。
△ △ △
ふたたび本庄です。
奇しくも昨日、当会の通信講座の内容に関連して、楽器の音の高さの基準について質問をある方からいただきました。多少専門的になりますが、今回の話題に関わっていますので、調べたことを紹介します。
現在、世界中でオーケストラなどに広く用いられている調律の基準では、中央のド(C音)の上のラ(A音)が440ヘルツに定められています。この基準は1834年にドイツで決められたものでA440と呼ばれています。
しかし西洋の古い時代には、これよりもやや低い調律の基準が演奏で用いられることが多かったようです(日本の古い楽器も同様に、A440よりやや低い調律で作られているものが多いようです)。
バラ十字会の昔の資料を調べたところ、1秒に1回振動する超低周波を基音(開放弦)にして、渡辺さんが今回書かれていたのと同じ、1オクターブ上の倍音を求めるという操作が繰り返されていました。
これを8回繰り返すと256ヘルツの音が得られますが、これを中央のド(C音)に定めるという調律の方法があります。
計算してみたところ、この場合のA音は純正律では426.7ヘルツ(256*5/3)、平均律では430.5ヘルツ(256*2^0.75)とA440よりも少しだけ低くなります。
古い時代に、一秒がどれほど正確に定められていたのかは分かりませんが、もしかしたらこの基準が、昔は使われていたのかもしれません。
今回も、最後までお読みくださり、ありがとうございました。
またお付き合いください。
追伸:メールマガジン「神秘学が伝える人生を変えるヒント」に、こちらから登録すると、このブログに掲載される記事を、無料で定期購読することができます(いつでも配信解除できます)。










コメントは受け付けていません。